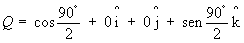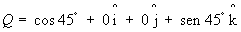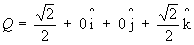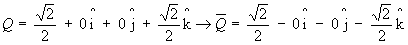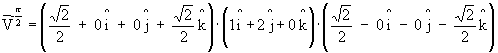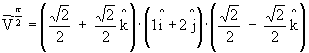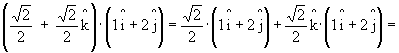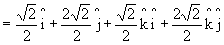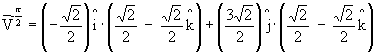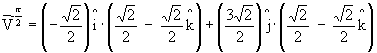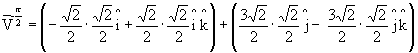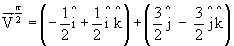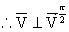Computação Gráfica - Profa Aura Conci
Aluno: Marcello J. Q. Pinheiro
Pesquisa sobre Quaternions
Introdução
Matrizes
A idéia de matriz estava implícita nos quaternions desde sua criação pelo matemático irlandês William Rowan Hamilton (1805-1865) em 1853, mas o mérito da invenção das matrizes é conferido ao matemático inglês Arthur Cayley (1821-1895). Ele declarou que chegou à idéia de matriz " ou diretamente a partir da idéia de determinante; ou como um jeito mais conveniente de representar as equações x I = a x + b y, y I = c x + d y ". Na teoria dos quaternions desenvolvida por Hamilton foi mostrado que era possível existir um sistema lógico no qual a multiplicação não fosse comutativa. Este primeiro resultado indubitavelmente foi fundamental para Cayley, no desenvolvimento de seu cálculo matricial, porque a multiplicação de matrizes também não é comutativa.
A teoria das matrizes de Cayley surgiu a partir de seu interesse por transformações lineares e invariantes algébricos, um interesse que ele compartilhou com o matemático inglês James Joseph Sylvester (1814-1897) considerado o fundador dos estudos matemáticos nos Estados Unidos da América. Ambos investigavam expressões que permaneciam invariantes (inalteradas exceto, eventualmente, por um fator constante) quando as variáveis eram transformadas por substituições representando translações, rotações, dilatações, expansões, contrações, reflexões em torno de um eixo e até a mudança de forma de um objeto.
1. Quaternion ![]()

Parte escalar Parte vetorial
2. Conjugado do quaternion ![]()
Números hipercomplexos
O matemático alemão Hermann Grassmann (1809-1877), em sua publicação "Ausdehnungslehre" de tradução livre "Expansão-pedagógica" em 1844, discutiu espaços n dimensionais e desenvolveu álgebras para esses sistemas. Essa nova concepção lhe permitiu considerar uma extensão dos números complexos aos números hipercomplexos. O matemático italiano Girolamo Cardano (1501-1576) foi o primeiro a considerar a possibilidade de representar as raízes de números negativos, mas quem introduziu a nomenclatura com os termos "real" e "imaginário", foi o advogado francês René Descartes (1596-1650) e o termo "número complexo" é devido ao matemático alemão Carl Friedrich Gauss (1777-1855).
Quaternions
Vetores produzem vetores quando são somados, subtraídos, multiplicados por um número real e multiplicados entre si, no caso do produto vetorial, mas não podem ser divididos. A preocupação com a ausência de qualquer conceito de quociente de vetores e o desejo de ampliar as aplicações com o uso de um sistema que possibilitasse substituir os vetores em todas as suas aplicações, fez com que o matemático irlandês William Rowan Hamilton (1805-1865) em 1853 desenvolvesse o conceito de números hipercomplexos que ele denominou de quaternions. Recentemente muitos físicos, matemáticos e engenheiros têm tentado reescrever as leis da Física utilizando os quaternions, que foram abandonados no século seguinte ao de sua criação e desapareceram completamente até o primeiro quartel do século passado. Hoje os matemáticos estão interessados em estudar sistemas de números em sua totalidade, em aprender suas propriedades e construir novos sistemas que tornem possíveis aplicações até agora restritas ao uso da Álgebra Tensorial tradicional. O sistema dos quaternions é por enquanto, a única álgebra de divisão associativa não comutativa sobre o corpo dos reais.
3. Operações com quaternions
3.1. Adição
![]()

3.2. Subtração
![]()


3.3. Multiplicação
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
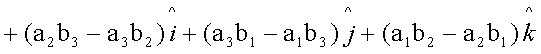
![]()
Produto escalar Produto vetorial
Usando a regra da mão direita
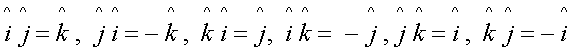

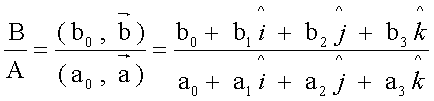
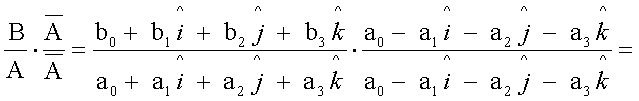
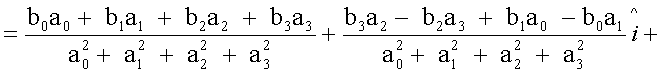
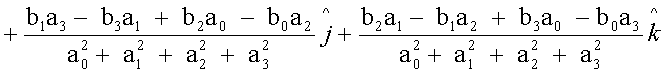
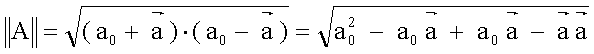
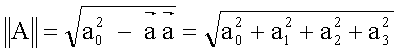
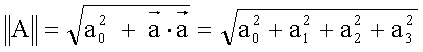
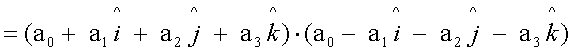
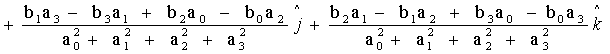
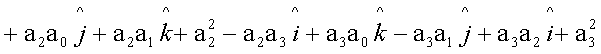
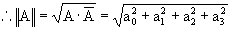
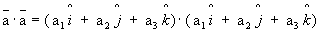
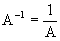
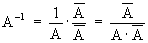
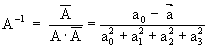
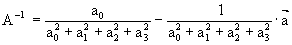
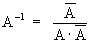 e
e 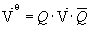 onde
onde 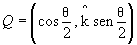
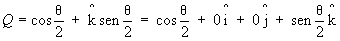
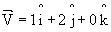 :
: