 | 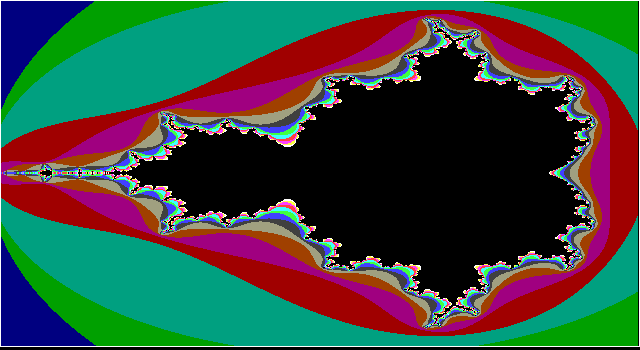 Mandelbrot |
0 - Fractal -> Benoit Mandelbrot introduziu o termo Fractal em 1975 para denominar uma classe especial de curvas definidas recursivamente que produziam imagens reais e surreais. Uma estrutura geométrica ou fÃsica tendo uma forma irregular ou fragmentada em todas as escalas de medição.
1 - Geometria Fractal -> Estuda subconjuntos complexos de espaços métricos. Na geometria de fractais determinÃsticos, os objetos estudados são subconjuntos gerados por transformações geométricas simples do próprio pbjeto nele mesmo. O objeto é composto por partes reduzidas dele próprio
 |
 |
 | img src="exetoy.gif"> |
3 - Iteração -> São cada uma das iterações dos Sistemas Dinâmicos, ou seja cada uma das suas repetições. Na biologia representa uma repetição sucessiva do processo ou uma geração.
4 - Ãrbitas -> São os resultados sucessivos das iterações sucessivas (os seus valores sucessivos ). Se o sistema dinamico produzir pontos é chamada de órbita cada um desses ponto.
5 - Ãrbita Estável -> São os resultados dos Sistemas Dinâmicos que convergem ao final do processo.
6 - Sistemas Dinâmicos Estável ou Instaveis -> São os que tem órbitas estáveis ou instáveis respectivamnete. O conjunto de pontos cujas órbitas são instáveis são chamadas de Conjuntos Caóticos. Fractais são conjuntos caóticos dos sistemas dinâmicos, por exemplo os conjuntos de Julia de Mandelbrot são figuras geradas pelas orbitas caóticas de um sistema dinamico. Os conjuntos de Julia estão estritamente conectados ao conjuntos de Mandelbrot. Esses conjunto são o resultado da iterações do sistema definido pela função: { cx = x * xscale + left e cy = y * yscale + top } onde x e y representamas partes real e imagináriade um n
úmero.
Para Julias no lugar de ( cx, cy ) coloca-se ( zx, zy ) e cx = parte real da constante que você quer usar (por exemplo 0.11031), cy = parte imaginaria da constante que você quer usar (por exemplo 0.67037). Cada conjuntos de Julia esta associado com cx e cy de determinado um ponto genérico de Mandelbrot.
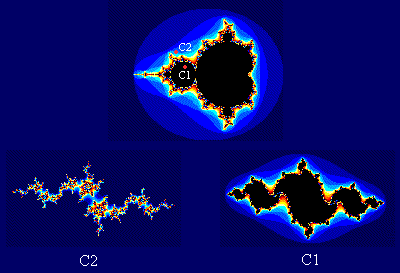 |  |
 Julia n.7 |  Julia n.6 |  Julia n.10 |  Julia n.11 |
7 - Conjunto Caótico no Plano -> O Mapa de Hénon é a execução de um processo de dois parâmetros ( duas variáveis ) repetidas vezes.
 Mapa de Hénon |
8 - Caos -> à a condição de não previsibilidade de determinados fenômenos, tanto da natureza quanto através de uma expressão matemática.
 |  |
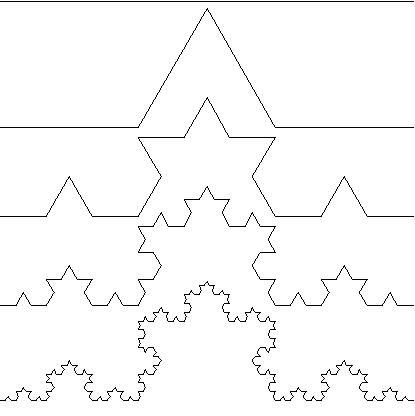
9 -Fractal Floco de Neve -> Proposta por Von Koch em 1904, tem a seguinte geração: desenhe uma linha e a divida em 3 partes iguais (d = 1/3 * r) d= escala da reta e r= comprimento inicial depois faça o terço central da reta ser substituindo por dois pedaços, repita o processo infinitamente.
 |
10 - Curva de Peano -> Conhecida também como "curva de Hilbert" é mostrada na figura abaixo.
 |
11 - Espaços das Fractais -> A fractal é um elemento do espaço dos fractais. Um expaço X é um conjunto e os pontos do espaço são os elementos do conjunto. Exemplo de conjunto: X = R (conjunto dos números reais) e Exemplo de ponto: x pertence R ( é um número real, um ponto na reta). -Um Espaço é Linear: quando a adição de dois elementos do espaço também pertence ao espaço. E a multiplicação de um elemento do espaço por um escalar também pertence ao espaço. - Espaço é chamado Vetorial quando ele é Linear, ou seja espaços lineares e vetoriais são sinônimos. O simbolo: A/B indica os membros do conjunto A que não são membros de B. - Espaços Métricos são espaços vetoriais que tem uma noção de distância entre dois pontos chamadas de métrica. à denotado por: Em outras palavras é um espaço X com uma função de valores reais, que mede a distância entre dois pontos (d = métrica). - Transformações : são associações entre pontos de espaço. - Transformações ContÃnuas: são aquelas em que os pontos vizinhos permanecem vizinhos>p>
Geno de uma Figura: é o número de buracos (vazados ) de uma figura ou de uma figura na qual ela possa ser transformada por uma transformação continua, ou seja através de uma função contÃnua. Por exemplo o Geno do R2é zero, pois ele pode ser transformado em um esfera e esta tem Geno zero. - Geodésia: é o menor caminho entre dois pontos em um espaço. - Espaços Homeomórfos: dois espaços métricos (x1, d1) e (x2, d2) são homeomorfos se existir uma função { f:x1 -> x2} que transforme um deles no outro.
{d: X x X -> R}
12 - Transformação na Reta -> à a transformação em um espaço métrico (X,d) é uma função f : X -> X que relaciona exatamente um ponto f(x) pertence X a cada ponto x pertence X.
13 - Transformação Afim -> R é uma transformação na forma : f(x) = ax + b onde a e b são constantes reais.
14 - Transformação Polinomial -> F : R -> R de grau N pode produzir até (n-1) dobras. Quando desejar obter um efeito especial em uma imagem "Dobrar a Imagem", basta utilizar a fórmula da transformação polinomial.
15 - Transformação Linear -> à a transformação afim em que t = 0, transformam paralelograma em paralelograms com origens no mesmo ponto.
16 - Transformação de MÃBIUS -> Esta transformação mapeia o plano complexo na esfera, conhecida como projeção estereográfica. Exemplo tÃpico são as bolas de Natal que espelham o que está de fora para dentro delas (Inversão na esfera).
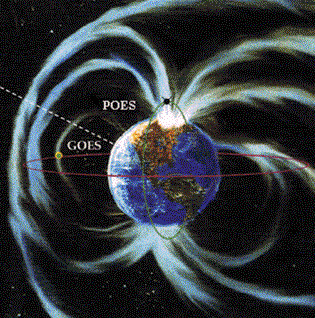 Trans.MÃBIUS |
Usam sistemas de funções para descrever as transformações que ocorrerão no conjunto inicial.
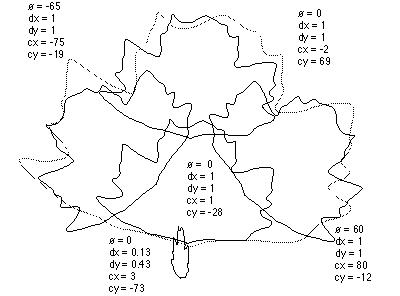
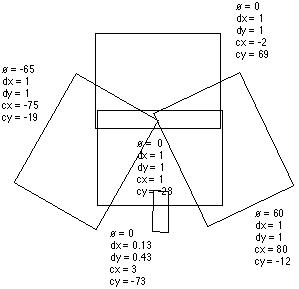
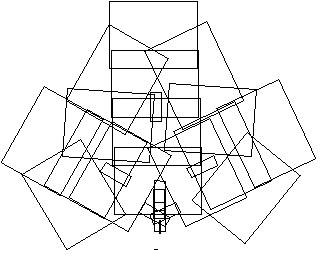
Exemplo mais tipico é o da geração folha de samambaia: O sistema gerado por um algoritmo semelhante mas ramdomico ("Random Iteration Algorithm" ) funciona calculando repetidamente séries de orbitas descrevem as posições de um ponto de coordenadas x y. Gerando uma samambaia.
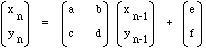 |
 |  |  |
 | 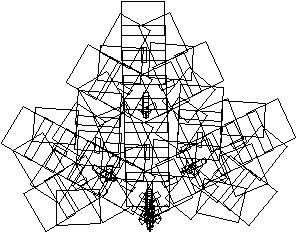 | 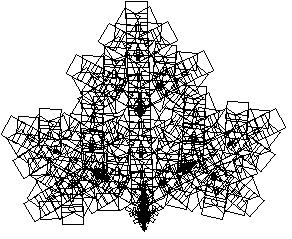 |
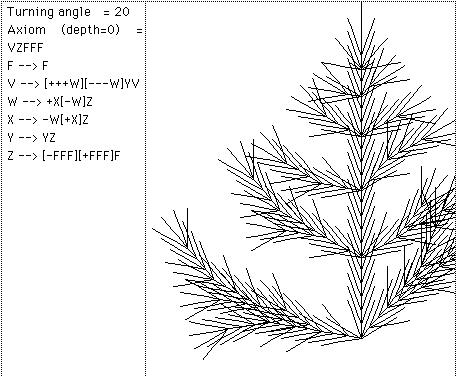
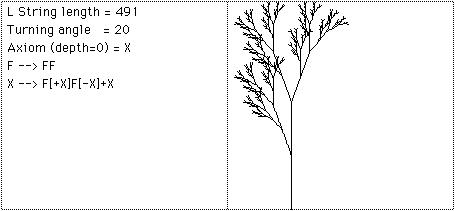
20 - L-System ou "Sistemas de Lindenmeyer" -> à uma ferramenta muito util para a criação de objetos realÃsticos que acontecem na natureza em particular estruturas de ramificação de plantas.
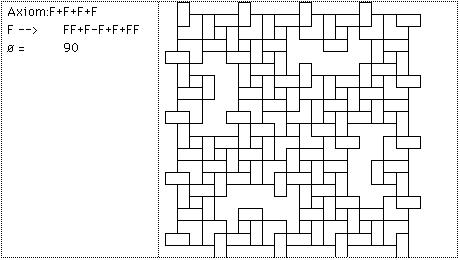
Tivemos aqui na UFF nos ultimos anos dois trabalhos de fim de curso que trataram da implementação de sistemas deste tipo. Um deles levou a geração so software EasyTree para geração de arvores, plantas e arbustos. O outro possibilita a geração tridimensional atraves de gráficos tartaruga de objetos. Um sÃmbolo ou objeto é gerado a cada repetição de acordo com algumas regras de substituição. Suponha que F quer dizer avance e desenhe uma linha reta, e Suponha que - quer dizer gire para a esquerda de 90 graus. Por exemplo: F+F+F+F e uma regra que dica para voce reescrever cada F por uma outra seguencia F -> F+F-F-FF+F+F-F depois de uma repetição resultaria a linha seguinte : F+F-F-FF+F+F-F + F+F-F-FF+F+F-F + F+F-F-FF+F+F-F + F+F-F-FF+F+F-F para a próxima repetição a mesma regra seria aplicada ... e o resultado : F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-FF+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-FF+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-FF+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-FF+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F+ F+ F-F-FF+ F+ F-F-F+ F-F-FF+ F+ F-F Usando outras regra de substituição diversas figuras podem ser geradas como as mostradas na figura seguinte:
Suponha que + quer dizer gire de 90 graus para a direita
 |  |  |
 |  |  |
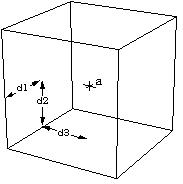
21 - Dimensão Euclidiana -> - Um objeto de 1 dimensão (por exemplo uma linha), pode ser dividido em N partes , cada parte será idêntica a anterior multiplicada por um fator ( r = 1/N e N * r1 = 1 ). - Um objeto de 2 dimensões (por exemplo um quadrado), cada parte será idêntica a anterior multiplicada por um fator ( r = 1/N e N * r2=1). - Um objeto de 3 dimensões (por exemplo um cubo), cada parte será idêntica a anterior e a original multiplicada por um fator ( r = 3v 1/N e N * r3=1 ).
 |  |  |
22 - Dimensão Fractal-> à obtida por medições experimentais como indicado no resumo do CD deste curso (cap.5), ou por deduções. Em imagens e texturas utiliza-se da técnica de Box Counting para determinação da dimensão fractal do objeto,essa técnica vem sendo pesquisado na UFF desde 1994 e já deu origem a diversos trabalhos, papers, disertações e teses. Atualmente a DF esta sendo pesquisada para catacterizar texturas multi bandas de imagens genéricas da superficie terrestre. A lacunariade é um aspecto que complementa a DF na caracterização de texturas.
Em ambos os casos são obtidos por a subdivisão sucessiva da figura cuja dimensao se deseja calcular. A Dimensão Fractal aproximada do clássico conjunto de Cantor pode ser obtida lembrando seu processo de geracao.
Como ele é gerado atraves da subdivisao de uma reta em 3 partes iguais, e cada iteração é igual a duas partes da próxima iteração. Vemos que precisamos de duas partes para reconstruir o todo e cada parte é igual a anterior dividida por 3. Esse exemplo,a dimensao do conjunto será ln 2/ ln 3.


- leia mais.... -