

CodificaçãoFractal / Fractal Coding
last modification : 08/03/98
Com o crescimento dos bancos de imagens e o uso cada vez mais intenso de redes, as necessidades de armazenamento e transmissão eficientes de imagens tornaram-se maiores. Várias são as formas de armazenar imagens eficientemente. A codificação fractal pode ser considerada mais uma destas formas. Este linha de pesquisa tem o objetivo de testar algumas formas, deste tipo de codificação e introduzir novas metodologias.
Já foram comparadas, em imagens monocromáticas, as técnicas de compressão fractal:
1- Busca Exaustiva,
2- Busca Exaustiva Leve,
3- Sub Busca Local,
4- Busca Local,
5- Busca Unitária,
6- Busca em Área Restrita,
7- Dimensão Fractal Local,
8- Dupla Classificação Canônica,
9- Classificação Canônica através da Intensidade,
10-Dupla Classificação Canônica com Quadtree de 3 níveis.
Em imagens coloridas foram comparadas as técnica de Sub Busca Local com passo D = 4 nos espaços de cores YIQ (utilizando a correlação entre os canais de cores) e RGB (com e sem a utilização da correlação entre os canais de cores).
As técnicas 2 a 7 acima foram implementadas no programa base de compressão fractal por Busca Exaustiva de Bansley. As técnicas 8 a 10 foram analisadas a partir do programa implementado por Fisher (http://inls.ucsd.edu/y/Fractals).
Compara-se as técnicas utilizando 2 conjuntos de imagens de teste, um para as imagens coloridas e outro para as imagens em tons de cinza. Os parâmetros de comparação usados são:
With sprouting of the image banks and the more intense use of nets, the necessities of efficient storage and transmission of images have been increased. Several new technologies have appeared in this direction. Fractal codification can be considered one of these. This research implements methodologies suggested in other works and introduces new methodology that uses concepts related with the local fractal dimension of images.
On grayscale images, the techniques of fractal compression implemented are:
1- Brute Force,
2- Light Brute Force,
3- Local Sub Search,
4- Local Search,
5- Look Same Place Search,
6- Restricted Area Search,
7- Local Fractal Dimension,
8- Double Canonic Classification,
9- Canonic Classification through Intensities,
10-Double Canonic Classification with Quadtree of 3 levels.
On color images the technique of Local Sub Search with step D = 4 has been used in the spaces of colors YIQ (using the correlation between channels of colors) and RGB (with and without the use of the correlation between the channels of colors).
The techniques 2 to 7 have been implemented in the base program of fractal compression by Brute Force (Barnsley). The techniques 8 to 10 have been analyzed from the program implemented by Fisher (http://inls.ucsd.edu/y/Frac).
The comparison uses 2 sets of test images, one for color images and another one for the grayscale images, leading in consideration
Geração de Fractais com o Auxílio do Teorema da Colagem
Uma imagem fractal pode ser vista como uma união de cópias reduzidas dela mesma. Cada cópia é obtida pela aplicação de um mapeamento de contração wi do SFI ( Sistema de Funções de Interação).
Restringindo-se à SFIs compostos por transformações afins no plano Euclidiano, os coeficientes da matriz A e do vetor coluna t poderão ser determinados através da simples determinação da posição onde três pontos da imagem original serão mapeados em cada cópia reduzida.
O Teorema do Mapeamento de Contração garante que partindo de qualquer conjunto inicial (imagem inicial) será encontrado o mesmo atrator para um determinado SFI.
Como exemplo, este teorema será aplicado na construção de um fractal muito conhecido, o Triângulo de Sierpinski.
Com X = [0,1]2 , parte-se de um conjunto inicial A0 = {quadrado de lados = 1} e um SFI formado pelas seguintes transformações:
w1 (x,y) = (½ x , ½ y ) ,
w2 (x,y) = (½ x + ½ , ½ y) , e
w3 (x,y) = (½ x + ¼ , ½ y + ½)
A figura abaixo mostra as primeiras iterações do processo de construção do Triângulo de Sierpinski.



1a iteração 2a iteração 3a iteração

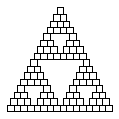

4a iteração 5a iteração Aproximação do Atrator !
Geração do Triângulo de Sierpinski através de IFS
Observando o Triângulo de Sierpinski pode-se notar que ele é formado por 3 cópias reduzidas dele mesmo, ou também, por 9 cópias reduzidas. Aplicando-se o Teorema da Colagem no Triângulo de Sierpinski, obtém-se as transformações e o seu código SFI. O código SFI é formado pelos parâmetros das transformações obtidas pelo Teorema da Colagem.
Pelo Teorema da Colagem uma imagem semelhante pode ser obtida cobrindo-se a imagem que será codificada com cópias reduzidas dela mesma, e quanto menor a quantidade de espaços em branco, sem alguma cópia o cobrindo, mais semelhante será a imagem obtida. Será utilizada uma transformação para cada cópia reduzida da colagem, indicando onde e como esta cópia será posicionada. Escolhe-se, geralmente, o menor número de cópias que ofereçam uma boa colagem da imagem. Neste caso, serão 3 cópias, que fornecerão uma colagem "perfeita", sem perdas, do Triângulo de Sierpinski.
A compressão de uma imagem gerada por um algoritmo fractal pode ser "perfeita", chegando a taxas de compressão extremas. Pela característica de um fractal ser auto-similar em diferentes escalas, uma imagem de 256 x 256 pixeis pode ter o mesmo código SFI de uma imagem de 512 x 512 pixeis ou qualquer outra dimensão. De acordo com esta consideração imagens de maiores dimensões terão taxas de compressão mais altas que as imagens de menores dimensões.
O Triângulo de Sierpinski pode ser gerado por um SFI (sem probabilidades associadas) com apenas três transformações. Considerando que cada transformação possui 6 parâmetros, tem-se então uma imagem codificada por 18 parâmetros, ou, pensando em tamanho de arquivo de imagem, e considerando que cada parâmetro pode ser definido por um byte, tem-se 18 bytes. Se o fractal estiver sendo gerado em uma imagem de 512 x 512 pixeis obtém-se 262.144 bits ou pixeis, ou 32.768 bytes sendo codificados com apenas 18 bytes, ou seja, uma taxa de compressão de 1.820,44/1, ou 0,0005493 bbp (bits por pixel). Caso o fractal seja gerado em uma imagem de 256 x 256 pixeis (65.536 pixeis ou bits, ou 8.192 bytes) a taxa de compressão será a seguinte 455,11/1 ou 0.0021972 bbp.
Chama-se SISTEMA DE FUNCOES DE ITERACAO PARTICIONADA :SFIP ao sistema de funções de iteração, que ao invés de partir de uma imagem semente e fazer cópias reduzidas desta, parte de regiões de uma imagem e os mapeia em regiões menores desta mesma imagem. Este sistema recebe o nome de Sistema de Funções de Iteração Particionado (SFIP), devido a peculiaridade de utilizar somente partes da imagem.
O SFIP possui como principal característica o estabelecimento de correlações de longa distância entre partes da imagem. Esta correlação é que define a característica fractal da imagem, estabelecendo auto-similaridades entre partes em diferentes escalas da imagem. Caso as dimensões das regiões sejam pré-estabelecidas e fixas, tem-se o conhecimento do número de funções que comporão o sistema, pois, como descreve-se adiante, a imagem será dividida em um número de regiões que dependerá somente do tamanho escolhido para estas regiões e as dimensões da própria imagem. Este mapeamento é chamado de não adaptativo, pois não permite uma variação dinâmica nas dimensões dos blocos molde.
Na compressão automática, utiliza-se os conceitos dos Sistemas de Funções de Iteração Particionados, que buscam a auto-similaridade entre partes maiores e partes menores da imagem. Desta forma, as imagens são vistas como uma colagem de partes auto similares que podem ser mapeadas entre si. Como partes menores toma-se blocos quadrados de n x n pixeis, chamados de blocos imagem ou molde, e como partes maiores blocos com o dobro das dimensões do menor (2n x 2n), chamados de blocos domínio. A abaixo mostra estes blocos. Os blocos são tradicionalmente escolhidos com forma quadrada por ter, este tipo de particionamento, um custo computacional relativamente mais baixo.

Formação de um par de blocos domínio-molde ótimo (Pulcini, Verrando, Rossi, Meloni, 1995).
Nesta compressão, a imagem deve ser entendida como um objeto tridimensional, o valor da tonalidade de um pixel (z) é tratado como sendo a terceira dimensão espacial. Os blocos tornam-se, na realidade, cubos ou figuras espaciais mais complexas, embora a denominação blocos permaneça (Komineck, 1995b).
O Teorema do Mapeamento de Contração é também aplicado a esta terceira dimensão, garantindo-se assim a convergência das tonalidades dos pixeis. A transformação afim abaixo será acrescentada ao sistema de funções de iteração bidimensional, tornando este tridimensional:
w(z) = s . z + o
onde:
s - é o coeficiente de variação do contraste. Se
s = 1 não há modificação no contraste;
s > 1 o contraste do bloco da imagem em questão é aumentado;
s < 1 o contraste do bloco da imagem em questão é diminuido;
s = 0 este bloco da imagem torna-se preto.
o - é o coeficiente de deslocamento (offset) da intensidade do pixel, ou seja, o deslocamento deste pixel ao longo do eixo z. Se
o = 0 não há deslocamento na intensidade do pixel;
o > 0 o pixel tem a sua intensidade aumentada, ou seja, sofre um deslocamento positivo no eixo z;
o < 0 o pixel tem a sua intensidade diminuída, sofrendo um deslocamento negativo ao longo do eixo z.
Cada uma das transformações afins tridimensionais toma a seguinte forma :
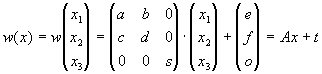
Considerando a imagem um ente tridimensional ( R3 ), se os mapeamentos de um sistema de funções de iteração, wi , são de contração, então quaisquer dois pontos no plano da imagem, depois de transformados, movem-se de forma a se aproximar espacialmente e em suas tonalidades.
d tonal (wi(u),wi(v)) < s i, tonal . d tonal (u, v) , 0 < = s i, tonal < 1
d geom (wi(u),wi(v)) < s i, geom . d geom (u, v) , 0 < = s i, geom < 1
onde:
u, v - são dois pontos quaisquer;
s i, tonal - é o fator de contração das tonalidades (no eixo z) do mapeamento;
s i, geom - é o fator de contração espacial do mapeamento;
d tonal - é a métrica usada para as tonalidades;
d geom - é a métrica usada espacialmente.
O código de representação SFIP de uma imagem, na implementação feita por Barnsley e Hurd, consiste de uma sequência de tuplas, uma por bloco :
wi = ( e i , f i , m i , o i , s i ).
onde:
ei - determina a translação do bloco domínio reduzido no eixo x;
fi - determina a translação do bloco domínio reduzido no eixo y;
mi - define a simetria do bloco domínio que possui a menor distância para o bloco range corrente, na métrica utilizada (será melhor explicada no próximo item);
oi - determina o deslocamento que o bloco domínio deverá receber no eixo z (mudança do valor da intensidade média);
si - determina o fator de contração espacial do mapeamento.
Considerações sobre a partição da imagem utilizada no SFIP
Uma imagem pode ser particionada em regiões com várias formas: triangulares, retangulares, quadradas, poligonais.
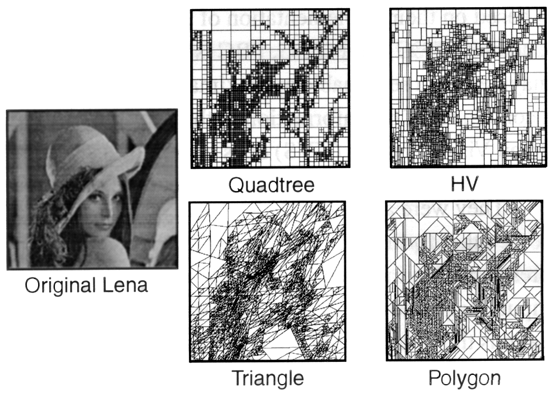
Diferentes formas de particionamento de uma imagem.
Considerações sobre a simetria do bloco domínio
Para cada bloco domínio tem-se 8 simetrias que serão testadas em relação ao bloco molde corrente. As simetrias são obtidas através da rotação e reflexão do bloco domínio reduzido. Para uma representação mais otimizada destas simetrias é possível considerar somente três operações, que aplicadas, em sua forma simples ou em composição, no bloco domínio reduzido resultarão nas simetrias da figura abaixo. As operações são:
Como tem-se oito simetrias e três operações de simetria, três bits são suficientes para representá-las, pois 23 = 8. Considera-se então o bit menos significativo como o responsável pela indicação de existência de reflexão horizontal, o bit intermediário como o responsável pela indicação de reflexão vertical, e finalmente o bit mais significativo como o responsável pela indicação de reflexão sobre a diagonal principal do bloco.
Utilizando esta convenção tem-se, as seguintes possibilidades:
(0,0,0) - Operação identidade
(0,0,1) - Reflexão em relação ao eixo horizontal
(0,1,0) - Reflexão em relação ao eixo vertical
(1,0,0) - Reflexão em relação à diagonal principal
(0,1,1) - Reflexão horizontal composta com reflexão vertical (rotação de 180° )
(1,0,1) - Reflexão horizontal composta com reflexão sobre a diagonal principal (rotação de 270° )
(1,1,0) - Reflexão vertical composta com reflexão sobre diagonal principal (rotação de 90° )
(1,1,1) - Reflexão horizontal composta com reflexão vertical e reflexão sobre a diagonal.
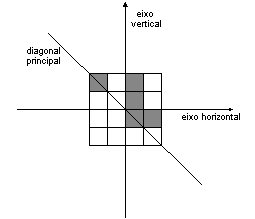
Eixos de Reflexão considerados nas operações de simetria.




Identidade - Rotacionada de 90 ° - Rotacionada de 180 ° - Rotacionada de 270 °
(0,0,0) - (1,1,0) - (0,1,1) - (1,0,1)




Reflexão horizontal - Reflexão horizontal da image rotacionada de 90 ° - Reflexão Vertical - Reflexão na diagonal
Procedimento básico de uma compressão automática
Na compressão fractal automática a imagem é dividida em blocos de várias dimensões, e é necessário saber, para cada um destes blocos, a sua posição absoluta dentro da imagem. Neste sentido, fica convencionado que a posição absoluta do bloco na imagem é a posição de seu primeiro pixel (mais à direita e acima) como exposto na figura abaixo:
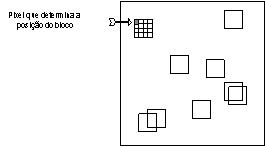
Posição absoluta dos blocos dentro de uma imagem.
A compressão fractal automática pode ser divida em 5 etapas.
Primeira etapa: ( Definição dos blocos molde )
Inicialmente divide-se a imagem a ser comprimida em uma malha de blocos quadrados homogêneos de dimensões n x n pixeis ( por exemplo 4 x 4 pixeis ). Estes blocos não podem se sobrepor, e foram originalmente chamados pelo criador do método de "range blocks". A figura abaixo ilustra esta divisão. Nela tem-se uma imagem de 32 x 32 pixeis dividida em blocos molde de 4 x 4 pixeis, dando um total de 32/4 x 32/4 = 82 = 64 blocos molde. Se esta imagem fosse de 512 x 512 pixeis, teríamos 512/4 x 512/4 = 1282 = 16.384 blocos molde. O número de blocos molde depende do tamanho da imagem e do tamanho dos blocos molde, sendo em uma imagem de M x N pixeis e blocos molde com dimensões fixas de n x n pixeis, codificação não adaptativa, igual à (M/n).(N/n).
Malha de blocos molde de uma imagem.
Segunda etapa: (Definição dos blocos domínio)
A mesma imagem é, em uma segunda etapa, novamente dividida em blocos quadrados com o dobro da dimensão dos blocos imagem, 2n x 2n (por exemplo 8x8 pixeis). Estes blocos maiores se sobrepõem, e receberam o nome de "domain blocks". A figura a seguir mostra estes blocos. Nela, a imagem de 32 x 32 pixeis é dividida em (32-8+1)2 = 289 blocos domínio. Uma imagem de 512 x 512 pixeis teria (512-8+1)2 = 255.025 blocos domínio. O número de blocos domínio de uma imagem (M x N pixeis) é igual à (M - 2n + 1).(N - 2n +1).
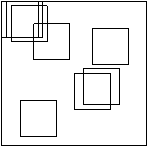
Alguns blocos domínio da figura anterior.
Terceira etapa: (Redução dos blocos domínio)
Para tornar possível uma comparação entre os dois tipos de blocos criados nas etapas anteriores, os blocos domínio de 2n x 2n pixeis terão as suas dimensões diminuídas da metade, passando a ter, então, n x n pixeis. A redução processa-se tomando sub-blocos de 2 x 2 pixeis, obtendo-se sua média, e atribuindo o valor da média quantizada ao pixel corresponde no bloco reduzido.
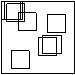
imagem reduzida por um fator igual a ½ , de onde sairão os blocos domínio reduzidos.
Quarta etapa: (Busca do melhor par bloco domínio reduzido-molde)
Esta etapa consiste na busca do bloco domínio reduzido mais próximo, na métrica considerada, de um bloco molde. Toma-se o primeiro bloco molde da imagem e utilizando uma métrica qualquer, por exemplo o erro rms, calcula-se a distância entre este bloco e todos os blocos domínio reduzidos e suas simetrias. Antes que se processe o cálculo da distância entre o bloco molde e o bloco domínio reduzido, este último ainda sofre um ajuste no offset (fator de deslocamento de intensidade - o ) que é obtido através da diferença entre as médias de intensidades dos dois blocos anteriores (domínio reduzido e molde).Temos 8 simetrias para cada bloco, e portanto serão feitos 8 testes para cada bloco domínio reduzido. Considerando por exemplo uma imagem de 32 x 32 pixeis teremos 8 x 289 = 2.312 testes à realizar para cada bloco molde e 64 x 2.312 = 147.968 para a imagem toda, e se a imagem tiver 512 x 512 pixeis teremos 8 x 255.025 = 2.040.200 para cada bloco molde, e 16.384 x 2.040.200 = 33.426.636.800 testes à realizar para toda a imagem. Serão armazenadas a posição e a simetria (mi) do bloco domínio que possuir a menor destas distâncias.
O valor do fator de deslocamento (oi) também será armazenado, e cada bloco molde passa a ser representado por uma tupla com a seguinte aparência:
Wi( Dx,Dy,m,o)
onde:
Dx - determina a posição ao longo do eixo x do bloco domínio reduzido
Dy - determina a posição ao longo do eixo y do bloco domínio reduzido
m - define a simetria aplicada ao bloco domínio reduzido
o - define o deslocamento ao longo do eixo z aplicado no bloco domínio reduzido.
As contrações tonais e espaciais são definidas como constantes neste algoritmo. A contração espacial está ligada a razão entre o tamanho dos blocos imagem (n) e domínio (2n), ou seja, é considerada ½ ; e a contração tonal é considerada como um valor constante arbitrário, como por exemplo 3/4.
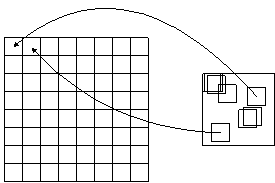
Formação dos pares ótimos entre os blocos domínio e molde.
Quinta etapa:
Repete-se a etapa anterior para cada um dos blocos molde. Armazenando-se as tuplas de cada bloco molde da imagem. O conjunto de todas estas tuplas será o código SFIP da imagem inteira.
Procedimentos automáticos otimizados
Na compressão com perda temos 3 fatores intimamente relacionados, que são:
O procedimento básico descrito acima representa a forma originalmente proposta para uma compressão automática, conhecida como "busca exaustiva" ou "força bruta". É um procedimento muito custoso e lento pois testa todos os blocos domínio reduzidos para cada bloco molde, sem considerar as características de cada bloco molde. Um bloco molde que possua, por exemplo, uma borda não precisaria ter em seu conjunto de blocos domínios reduzidos testados ("domain pool") aqueles que não possuíssem descontinuidades, ou altas freqüencias, características de bordas.
Várias técnicas de aceleração deste procedimento automático foram e estão sendo desenvolvidas. Técnicas que consideram as características de cada bloco molde, ou consideram propriedades de um dado conjunto de imagens, etc.
A seguir serão apresentadas algumas destas técnicas de aceleração do procedimento automático. Várias destas técnicas foram implementadas, para esta dissertação, num mesmo programa base, de modo a ser possível analisar suas características específicas em relação ao tempo de compressão e qualidade final da imagem processada. A utilização do SFIP considera o tamanho do arquivo comprimido como uma função do número de pixeis da imagem (M x N) e do tamanho dos blocos molde (n x n).
As técnicas de aceleração do procedimento automático que serão consideradas podem ser divididas em dois grupos básicos:
Estes dois grupos podem ser, também, subdivididos em alguns métodos específicos. Tem-se, então, para a primeira técnica os seguintes métodos:
1.1. Método de Busca Exaustiva Leve com passo D ;
1.2. Método de Busca Local;
1.3. Método de Sub Busca Local com passo D ;
1.4. Método de Busca Unitária;
1.5. Método de Busca em Área Restrita;
1.6. Método de Busca em Espiral Local.
A segunda técnica pode ser considerada com as seguintes subdivisões:
2.1. Armazenamento em estrutura de dados unidimensional, que, por sua vez, se dividirá em alguns métodos:
2.2. Armazenamento em estrutura de dados multidimensional, onde o armazenamento dos blocos domínio reduzidos é feito em uma árvore retangular multidimensional.
A primeira desta pode ainda ser divida em :
2.1.1 Método de classificação canônica através da média das intensidades dos quadrantes;
2.1.2 Método de classificação canônica através da média das variâncias dos quadrantes;
2.1.3 Método de dupla classificação canônica. Este representa uma combinação dos dois métodos anteriores, através da média das intensidades dos quadrantes, e da média das variâncias dos quadrantes;
2.1.4 Método de classificação através da detecção de bordas pelo filtro de Sobel;
2.1.5 Método de criação de agrupamentos;
O programa base (Barnsley e Hurd) utiliza o procedimento básico de "Busca Exaustiva" descrito no item anterior. Ele adota blocos molde de 4 x 4 pixeis e blocos domínio de 8 x 8 pixeis. Todas as modificações implementadas no programa base seguirão estas especificações, sendo que qualquer derivação será notificada.
As comparações pelos métodos implementados serão apresentados em colunas, da seguinte forma:
onde: ruído = diferença entre os pixeis correspondentes:imagem original - reconstrução;
5 ® é o mesmo fator multiplicativo do cálculo do erro anterior.
A equação utilizada na obtenção da última imagem garante que todos os valores obtidos para os erros serão positivos, e que os sinais do ruído estarão representados na imagem. Esta visualização das diferenças será chamada de erro relativo deslocado.
Considerações sobre os resultados obtidos pelos algorítmos fractais
Para avaliar a similaridade entre a imagem original e a imagem reconstruída (obtida pela descompressão do código obtido pelos respectivos algoritmos) necessita-se de uma medida quantificável de sucesso do processo de compressão. Esta é obtida através de um critério de fidelidade objetiva que permite que a perda de dados seja representada como uma função de ambas as imagens. As funções de avaliação utilizadas serão a Raiz quadrada do Quadrado da Média dos Erros (Root Mean Square Error - erms), a Relação Sinal Ruído (rms) (Signal to Noise Ratio - SNR), e a Relação Sinal Ruído de Pico (Peak Signal to Noise Ratio - PSNR), em decibéis.
Na função erms , dadas duas imagens de tamanho M x N pixeis, uma imagem original F(x, y) e uma imagem reconstruída G(x, y), tem-se que o erro e(x, y) entre elas para qualquer pixel (x, y) é dado por :
e(x, y) = G(x, y) - F(x, y)
então, a raiz quadrada do quadrado da média dos erros sobre todos os pixeis da imagem (M x N) fica definida por:
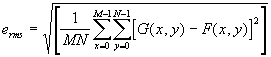
A Relação Sinal Ruído (ms - mean square, média dos quadrados) obedecerá à seguinte equação:
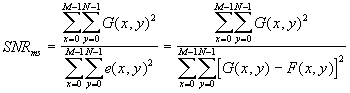
e a Relação Sinal Ruído rms à seguinte (Gonzalez, Woods, 1993):
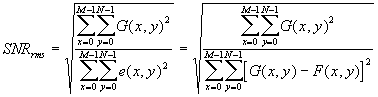
A relação Sinal Ruído de Pico, em decibéis (dB), é dada pela seguinte fórmula:
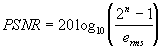
como n é uma constante definida pela quantidade de bits necessária para representar cada pixel da imagem, no presente caso igual a 8, pois utiliza-se imagens em tons de cinza variando de 0 à 255, tem-se que a relação toma a seguinte forma:
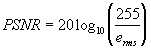
Através destas quantificações é possível comparar os méritos relativos as várias implementações selecionando qual delas é a melhor. É observado que a Relação Sinal Ruído de Pico (PSNR) é uma medida razoável da qualidade visual das imagens (dadas duas imagens reconstruídas, codificadas por diferentes métodos, a que apresentar o maior valor PSNR parecerá visualmente melhor). É claro, também, que a melhor codificação deverá ter a máxima compressão e a máxima fidelidade no menor tempo possível (Jacobs, Fisher, 1992).
Nos exemplos que se seguem serão utilizadas imagens com o mesmo número de pixeis e blocos molde e domínio com dimensões fixas, de modo que o tamanho do arquivo permanecerá constante em todas as técnicas. Para tornar clara as diferenças entre as imagens obtidas pela descompressão dos códigos de cada técnica utilizaremos 13 imagens de teste.
Resultado da implementação base
Mostra-se, agora, os resultados obtidos com a implementação original sem qualquer tipo de modificação com o programa base de Barnsley e Hurd para as imagens testes selecionadas. A taxa de compressão das imagens foi constante, pois manteve-se o tamanho das imagens e uma malha de blocos molde fixa (não adaptativa). Como todas as imagens de teste possuem dimensões de 128 x 128 pixeis, tem-se em cada uma 16.384 pixeis. O arquivo codificado obtido pelo programa base tem como resultado um arquivo de 7.172 bytes (57.376 bits). Desta forma, a taxa de compressão obtida pelo programa base será de 3, 5020 bpp.