 Figura
2
Figura
2CODIFICAÇÃO DA IMAGEM
By: Teresa Cristina Teixeira Vieira Carneiro
O principal objetivo da codificação de uma imagem é representá-la com o menor número possível de bits, preservando a qualidade e a inteligibilidade necessárias à sua aplicação. A codificação realiza uma compressão na imagem, facilitando sua transmissão e armazenamento.
Existem dois métodos principais de compressão:
Os algoritmos codificadores são classificados em três categorias, dependendo de que aspecto da imagem eles codificam:
O diagrama abaixo representa as etapas de codificação de uma imagem.
Imagem Þ Transformação Þ Quantização Þ Declaração do Código Imagem Codificada
A primeira etapa, denominada transformação, determina o que vai ser codificado.
Para representar a imagem com um número finito de bits, as intensidades da imagem, os coeficientes transformadores ou os parâmetros modeladores devem ser quantizados. A quantização estabelece níveis (valores), dentro de uma faixa determinada, para cada elemento da imagem.
A terceira etapa, chamada declaração do código, é a responsável pela codificação da quantização. Cada nível de quantização possui o seu código e, ao reconstruir-se a imagem, este código é verificado para determinar que nível de reconstrução deverá ser utilizado.
Se deseja-se transmitir mais do que um nível de reconstrução em seqüência, os códigos devem ser definidos de modo a serem reconhecidos em seqüência. Um código com estas características é dito unicamente decodável. Um código não unicamente decodável pode apresentar erros no momento da reconstrução da imagem. A tabela 1 apresenta um exemplo destes dois códigos.
|
Informação |
Unicamente decodável |
Não-unicamente decodável |
|
r1 |
00 |
0 |
|
r2 |
01 |
1 |
|
r3 |
10 |
10 |
|
r4 |
11 |
11 |
Tabela 1
No código não unicamente decodável ao se transmitir a mensagem 100 ela pode ser interpretada como a seqüência de informações r3 r1 ou r2 r1 r1.
O método mais simples de selecionar códigos é usá-los com um comprimento uniforme. Desta maneira todas as informações possuem o mesmo comprimento.
A tabela 2 apresenta um código com comprimento uniforme.
|
Informação |
Código |
|
r1 |
000 |
|
r2 |
001 |
|
r3 |
010 |
|
r4 |
011 |
|
r5 |
100 |
|
r6 |
101 |
|
r7 |
110 |
|
r8 |
111 |
Tabela 2
O número de bits necessários à codificação de uma informação é denominado taxa de bits. A taxa de bits no exemplo anterior é de 3 bits/informação. Se codifica-se mais do que uma informação a taxa de bits média é definida como o número total de bits dividido pelo número de informações. Para códigos de comprimento uniforme a taxa média e a taxa de bits são idênticas.
Códigos de comprimento uniforme, embora simples, em geral não são ótimos em termos de taxa média de bits. Suponha-se que algumas informações são mais transmitidas do que outras. Declarando códigos menores para as mensagens com maior possibilidade de serem transmitidas e códigos maiores para as de menor possibilidade, reduz-se a taxa média de bits.
CÓDIGO DE HUFFMAN
Um código simples de usar, que é unicamente decodável e que resulta na menor taxa média possível é o código de Huffman.
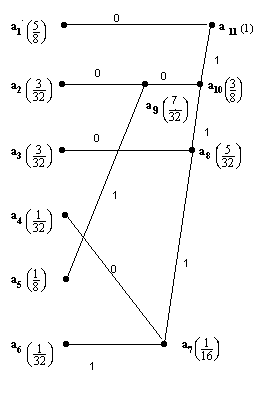
Um exemplo deste código é apresentado na figura 2, com 6 informações a serem transmitidas, cada qual com uma probabilidade de ocorrência.
As duas informações com a menor probabilidade são selecionadas. Neste caso elas são a4 e a6, cujas probabilidades de ocorrência são somadas, dando origem a uma nova informação a7, com probabilidade de ocorrência de 1/16 .
Os braços que unem a4 e a6 a a7 são designados 0 e 1. Invertendo as designações somente a declaração do código é afetada, mantendo-se a média dos bits.
Seleciona-se, a seguir, entre as mensagens a1, a2, a3, a5 e a7 as duas que possuem a menor probabilidade de ocorrência. Desta vez são a3 e a7 que, somadas, formarão a8. Continua-se o processo até que reste apenas uma informação, com probabilidade de ocorrência igual a 1.
 Figura
2
Figura
2
Para determinar o código específico de cada informação, percorre-se o caminho que leva até a mesma, a partir do ponto de probabilidade igual a 1, e combina-se os 0's e 1's de cada ramificação. Percorrendo-se todos os caminhos, chega-se aos códigos apresentados na tabela 3.
|
Informação |
Probabilidade |
Código |
|
a1 |
5/8 |
0 |
|
a2 |
3/32 |
100 |
|
a3 |
1/32 |
110 |
|
a4 |
1/8 |
1110 |
|
a5 |
1/8 |
101 |
|
a6 |
1/32 |
1111 |
Tabela 3
Analisando a tabela verifica-se que informações com probabilidades maiores possuem menor código e informações com probabilidades menores possuem maior código. O código de Huffman obtém uma taxa média de bits de 1,813 bits/informação, ao passo que, com o código de comprimento uniforme, esta taxa é de 3 bits/informação. Comprova-se, então, que o algoritmo de Huffman é um excelente código quanto se trabalha com imagens que possuem muitos elementos repetidos.