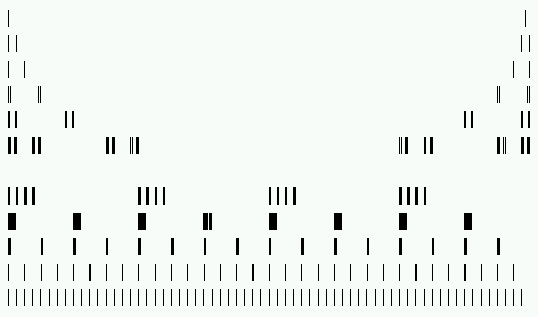
As propriedades e características de um conjunto fractal não são determinadas completamente por sua
dimensão D. Realmente, é fácil construir uma família de fractais que tenha, o mesmo D mas
com formas diferentes. Como um exemplo desta construção, a figura anterior descreve um grupo de modificacoes no conjunto de Cantor - "Cantor set"- ( o intervalo e' dividido em 4 partes e as 2 partes centrais removidas ) feito a partir de um gerador de intervalos e fator de redução.
Pela forma como foram construidos, todas tem a mesma D: log N/log(1/r) = log2/log4 .
A partir do conjunto superior
do medio, o índice k varia de 1 a 6 quando movemos para cima e de 1 a 5 quando baixamos. Abaixo do meio os segmentos sao uniformemente distribuidos; acima ele se aproximam do fim do conjunto. Os extremos nao parecem "fractals".
Estes conjunto tem "textura" diferentes, isso e diferentes lacunaridades.
Lacunaridade e uma caracteristica distinta e independente de D; ela nao se relaciona com a topologia do fractal
e necessita de mais de um valor numerico para ser perfeitamente determinado. A Lacunaridade se relaciona fortemente com a
distribuição e tamanho
dos buracos no fractal e com sua divergencia de um invariante a translacao (translational invariance); de maneira geral, um
fractal é muito lacunar se seus buracos tendem a ser grandes, no sentido de incluirem regiões grandes de
espaço.
Mas como calcular esta lacunaridade? A formula de lacunaridade
apresentada por Mandelbrot usa momentos de probabilidade de ordem um e dois.
O termo lacunaridade foi tambem introduzido por este autor e vem do latin "lacuna" que significa buracos ou "gaps". Ele tambem introduziu o uso do simbolo "^" para o valor da lacunaridade de um conjunto. E este e' obtido de:
^(L) = abs [ M2(L) - M(L)* M(L) ] / M(L) ]
onde M(L) e' o momento de ordem um e M2(L) o de ordem dois.
Assim, calcular a lacunaridade nos leva ao calculo dos momentos de probabilidade
de um conjunto, ou uma de imagem.
Como calcular os momentos de probabilidade de uma imagem?
Ou ainda como ver uma imagem como uma distribuicao de probabilidade?
Uma simulacao numerica ou uma imagem em preto e branco produz um objeto geometrico que e' definido pelo conjunto S de pontos . Estes pontos pretos sao representados pelas suas posicoes: x=(x1,x2) se o objeto for do plano (2D), ou x=(x1,x2,x3) se do espaco (3D), ou ainda x=(x1,x2,x3,....xn) se o objeto for do espaco Euclidiano de dimensao n.
Na falta de qualquer outra informacao, todos os pontos podem ser assumidos serem equivalentes e com igual probabilidade. Este arranjo espacial de pontos pode entao determinar uma probabilidade P(m,L).
Ou seja uma figura pode ser entendida como representada por uma probabilidade de existir m pontos dentro de um box de tamanho L centrado em um ponto arbitrario de S (que deve ser normalizada para
ser realmente uma probabilidade). Desta maneira o momento de ordem q da imagem
pode ser considerado como a somatoria dos momentos de cada um dos seus pontos de massa, e cada um destes momentos escritos como:
m = m * P (m, L) - momento de ordem 1 da massa m;
m2 = m * m * P (m, L) - momento de ordem 2 da massa m;
m3 = m * m * m * P (m, L) - momento de ordem 3 da massa m;
m4 = m * m * m * m * P (m, L) - momento de ordem 4 da massa m;
........
M1, M2, M3,.... seriam as somatorias de todos momentos de massa ( m1, m2, m3,...) de ordem 1,2,3,.... de todos os pontos de massa de uma imagem.
No capitulo 1 de Peitgen, H.O. and Saupe, D.
- The Science of Fractal Images, Springer-Verlag, New York, 1988. ( BCTC/UFF 006.6 - S416 1988 ), Voss ,o autor do capitulo, da' exemplo do calculo de M1,M2, M3, M4,.... para duas fractais: a curva floco de neve de Koch e uma coastline. Que tal reproduzir seus dados, para verificar se endente-se bem o sentido da lacunaridade de um conjunto?