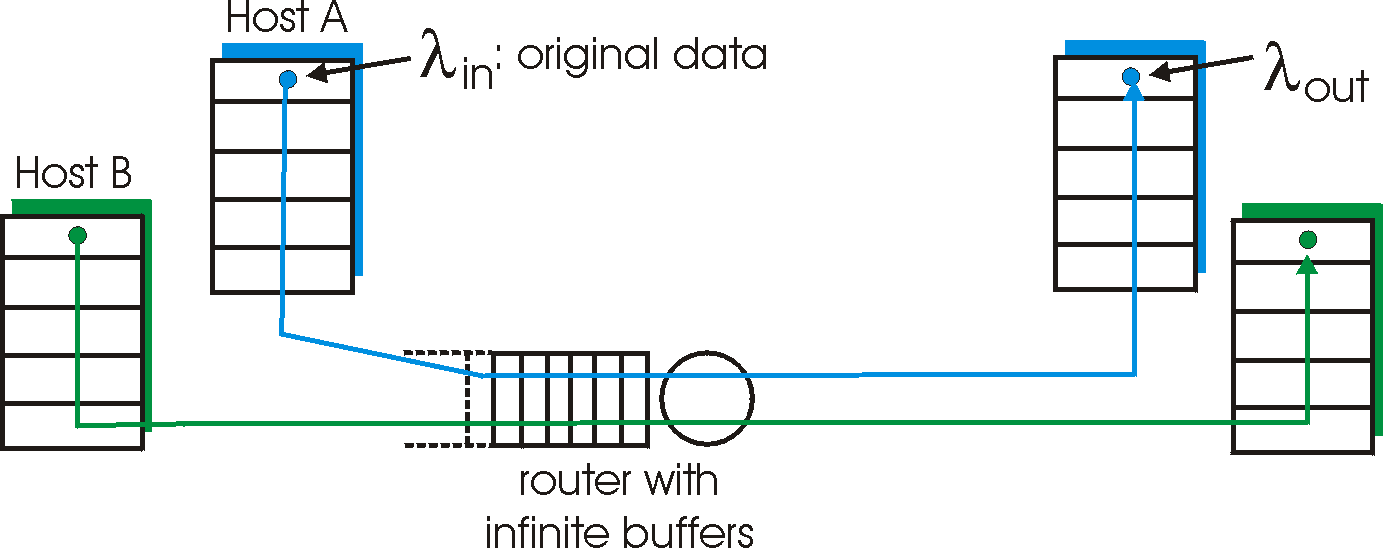
Figure 3.6-1: Congestion scenario 1: two connections sharing a single hop with infinte buffers
In this section, we consider the problem of congestion control in a general context, seeking to understand why congestion is a "bad thing," how network congestion is manifested in the performance received by upper-layer applications, and various approaches that can be taken to avoid, or react to, network congestion. This more general study of congestion control is appropriate since, as with reliable data transfer, it is high on the "top-10" list of fundamentally important problems in networking. We conclude this section with a discussion of congestion control in the ATM ABR protocol. The following section contains a detailed study of TCP's congestion control algorithm.

Let's assume that the application in Host A is sending data into the connection (e.g., passing data to the transport-level protocol via a socket) at an average rate of lin bytes/sec. These data are "original" in the sense that each unit of data is sent into the socket only once. The underlying transport-level protocol is a simple one: data is encapsulated and sent; no error recovery (e.g., retransmission), flow control, or congestion control is performed. Host B operates in a similar manner and we assume for simplicity that it too is sending at a rate of lin bytes/sec. Packets from hosts A and B pass through a router and over a shared outgoing link of capacity C. The router has buffers that allow it to store incoming packets when the packet arrival rate exceeds the outgoing link's capacity. In this first scenario, we'll assume that the router has an infinite amount of buffer space.
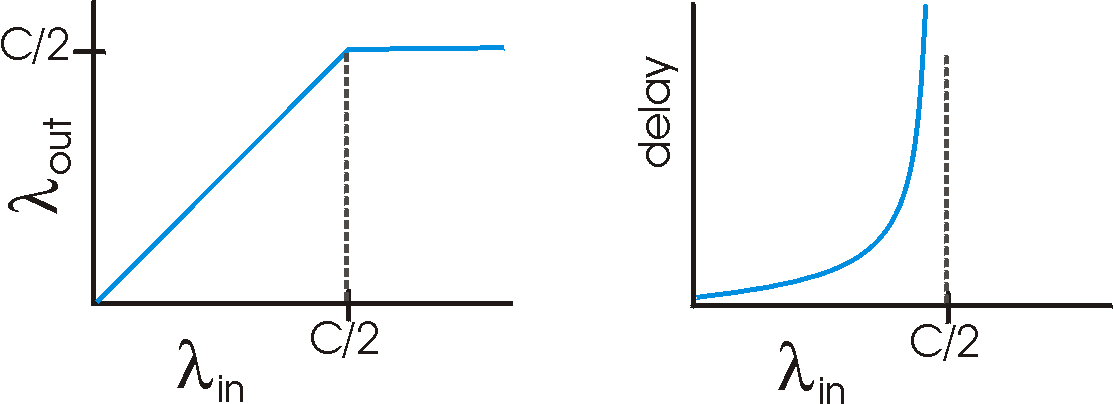
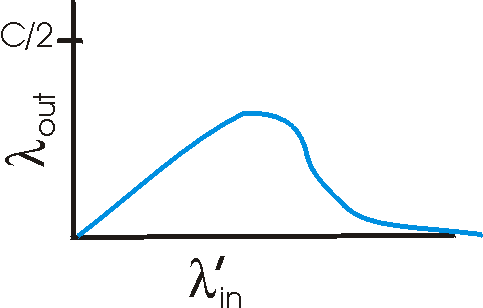
Figure 3.6-2 plots the performance of Host A's connection under this first scenario. The left graph plots the per-connection throughput (number of bytes per second at the receiver) as a function of the connection sending rate. For a sending rate between zero and C/2, the throughput at the receiver equals the sender's sending rate - everything sent by the sender is received at the receiver with a finite delay. When the sending rate is above C/2, however, the throughput is only C/2. This upper limit on throughput is a consequence of the sharing of link capacity between two connections - the link simply can not deliver packets to a receiver at a steady state rate that exceeds C/2. No matter how high Hosts A and B set their sending rates, they will each never see a throughput higher than C/2.
Achieving a per-connection throughput of C/2 might actually appear to
be a "good thing," as the link is fully utilized in delivering packets
to their destinations. The right graph in Figure 3.6-2, however,
shows the consequences of operating near link capacity. As the sending
rate approaches C/2 (from the left), the average delay becomes larger and
larger. When the sending rate exceeds C/2, the average number of
queued packets in the router is unbounded and the average delay between
source and destination becomes infinite (assuming that the connections
operate at these sending rates for an infinite period of time). Thus, while
operating at an aggregate throughput of near C may be ideal from a throughput
standpoint, it is far from ideal from a delay standpoint. Even
in this (extremely) idealized scenario, we've already found one cost of
a congested network - large queueing delays are experienced as the packet
arrival rate nears the link capacity.
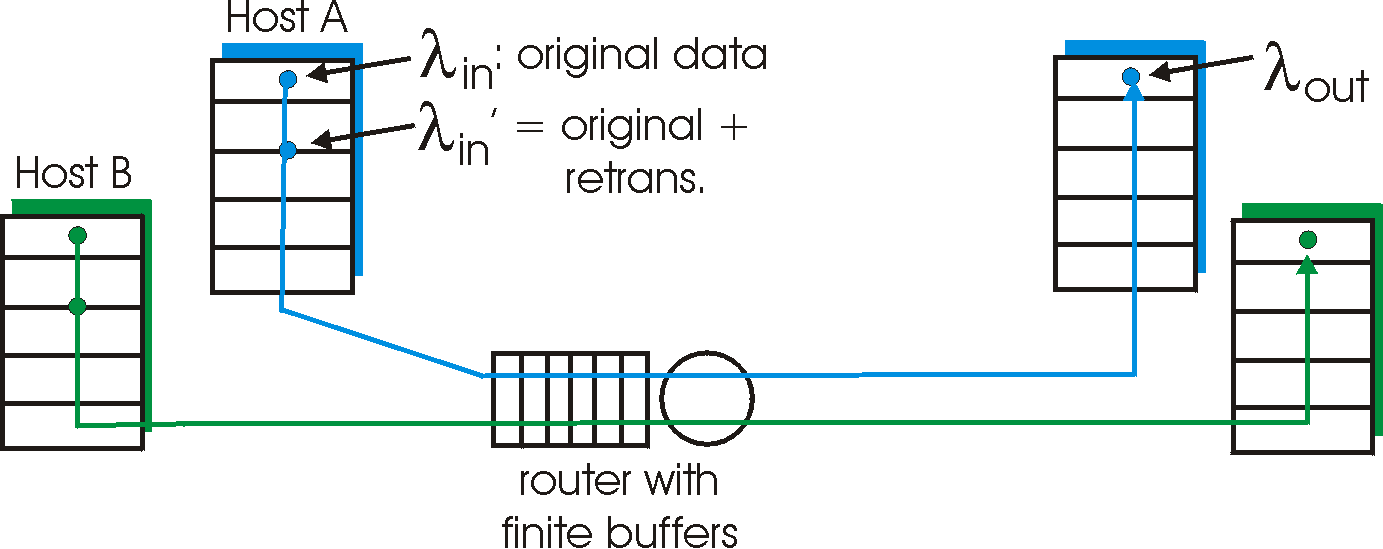
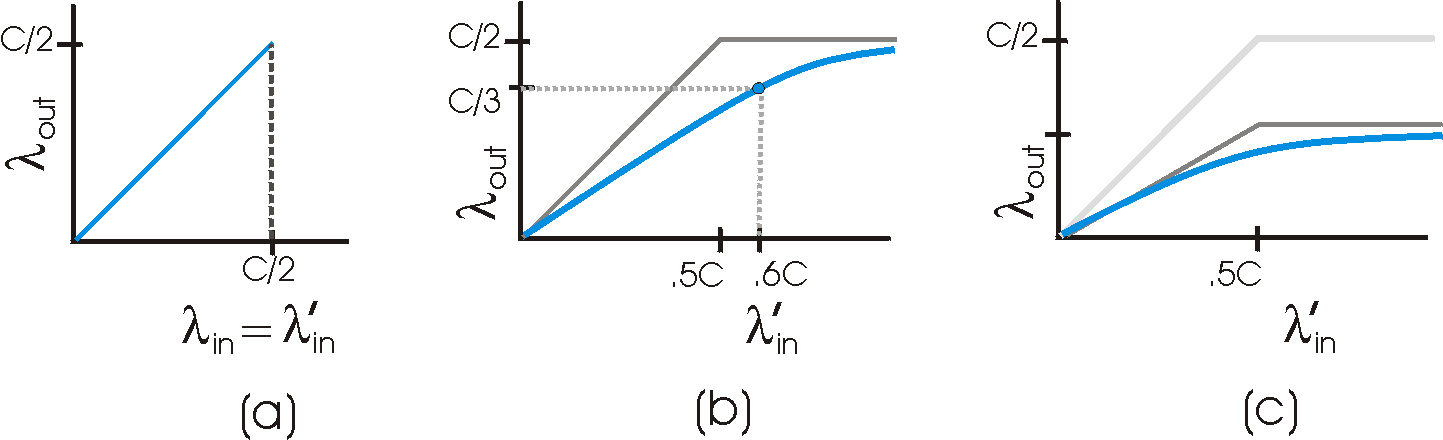
The performance realized under scenario 2 will now depend strongly on how retransmission is performed. First, consider the unrealistic case that Host A is able to somehow (magically!) determine whether or not a buffer is free in the router and thus sends a packet only when a buffer is free. In this case, no loss would occur, lin would be equal to lin ' , and the throughput of the connection would be equal to lin. This case is shown in Figure 3.6-4(a). From a throughput standpoint, performance is ideal - everything that is sent is received. Note that the average host sending rate can not exceed C/2 under this scenario, since packet loss is assumed never to occur.
Consider next the slightly more realistic case that the sender retransmits only when a packet is known for certain to be lost. (Again, this assumption is a bit of a stretch. However, it possiible that the sending host might set its timeout large enough to be virtually assured that a packet that has not been ACKed has been lost.) In this case, the performance might look something like that shown in Figure 3.6-4(b). To appreciate what is happening here, consider the case that the offered load, lin' (the rate of original data transmission plus retransmissions), equals .6C. According to FIgure 3.6-4(b), at this value of the offered load, the rate at which data are delivered to the receiver application is C/3. Thus, out of the .6C units of data transmitted, .3333 bytes/sec (on average) are original data and .26666 bytes per second (on average) are retransmitted data. We see here another "cost" of a congested network - the sender must perform retransmissions in order to compensate for dropped (lost) packets due to buffer overflow.
Finally, let us consider the more realistic case that the sender may
timeout prematurely and retransmit a packet that has been delayed in the
queue, but not yet lost. In this case, both the original data packet
and the retransmission may both reach the receiver. Of course, the
receiver needs but one copy of this packet and will discard the retransmission.
In this case, the "work" done by the router in forwarding the retransmitted
copy of the original packet was "wasted," as the receiver will have already
received the original copy of this packet. The router would
have better used the link transmission capacity transmitting a different
packet instead. Here then is yet another "cost" of a congested
network - unneeded retransmissions by the sender in the face of large
delays may cause a router to use its link bandwidth to forward uneeded
copies of a packet. Figure 3.6.4(c) shows the throughput
versus offered load when each packet is assumed to be forwarded (on average)
at least twice by the router. Since each packet is forwarded twice,
the throughput achieved will be bounded above by the two-segment curve
with the asymptotic value of C/4.
Let us consider the connection from Host A to Host C, passing through Routers R1 and R2. The A-C connection shares router R1 with the D-B connection and shares router R2 with the B-D connection. For extremely small values of lin , buffer overflows are rare (as in congestion scenarios 1 and 2), and the throughput approximately equals the offered load. For slightly larger values of lin , the corresponding throughput is also larger, as more original data is being transmitted into the network and delivered to the destination, and overflows are still rate . Thus, for small values of lin , an increase in lin results in an increase in l out.
Having considered the case of extremely low traffic, let us next examine the case that lin (and hence lin') is extremely large. Consider router R2. The A-C traffic arriving to router R2 (which arrives at R2 after being forwarded from R1) can have an arrival rate at R2 that is at most C, the capacity of the link from R1 to R2, regardless of the value of lin. If lin' is extremely large for all connections (including the B-D connection), then the arrival rate of B-D traffic at R2 can be much larger than that of the A-C traffic. Because the A-C and B-D traffic must compete at router R2 for the limited amount of buffer space, the amount of A-C traffic that successfully gets through R2 (i.e., is not lost due to buffer overflow) becomes smaller and smaller as the offered load from B-D gets larger and larger. In the limit, as the offered load approaches infinity, an empty buffer at R2 is immediately filled by a B-D packet and the throughput of the A-C connection at R2 goes to zero. This, in turn, implies that the A-C end-end throughput goes to zero in the limt of heavy traffic. These considerations give rise to the offered load versus throughput tradeoff shown below in Figure 3.6-6.
The reason for the eventual decrease in throughput with increasing offered
load is evident when one considers the amount of wasted "work" done
by the network. In the high traffic scenario outlined above, whenever
a packet is dropped at a second-hop router, the "work" done by the first-hop
router in forwarding a packet to the second-hop router ends up being "wasted."
The network would have been equally well off (more accurately, equally
as bad off) if the first router had simply discarded that packet and remained
idle. More to the point, the transmission capacity used at the first
router to forward the packet to the second router could have been much
more profitably used to transmit a different packet. (For example, when
selecting a packet for transmission, it might be better for a router to
give priorty to packets that have already traversed some number of upstream
routers). So here we see yet another cost of dropping a packet
due to congestion - when a packet is dropped along a path, the transmission
capacity that was used at each of the upstream routers to forward that
packet to the point at which it is dropped ends up having been wasted.
At the broadest level, we can distinguish among congestion control approaches based on the whether or not the network layer provides any explicit assistance to the transport layer for congestion control purposes:
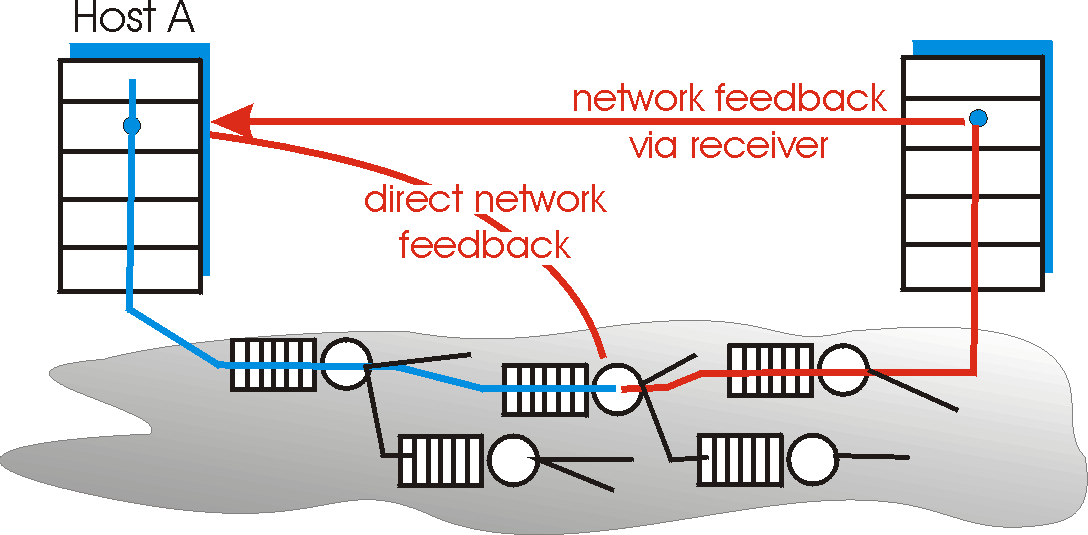
Figure 3.6-8 shows the framework for ATM ABR congestion control. In our discussion below we adopt ATM terminology (e.g., using the term "switch" rather than "router," and the term "call" rather than "packet). With ATM ABR service, data cells are transmitted from a source to a destination through a series of intermediate switches. Interpersed with the data cells are so-called RM (Resource Management) cells; we will see shortly that these RM cells can be used to convey congestion-related information among the hosts and switches. When an RM cell is at a destination, it will be "turned around" and sent back to the sender (possibly after the destination has modified the contents of the RM cell). It is also possible for a switch to generate an RM cell itself and send this RM cell directly to a source. RM cells can thus be used to provide both direct network feedback and network-feedback-via-the-receiver, as shown in Figure 3.6-8.
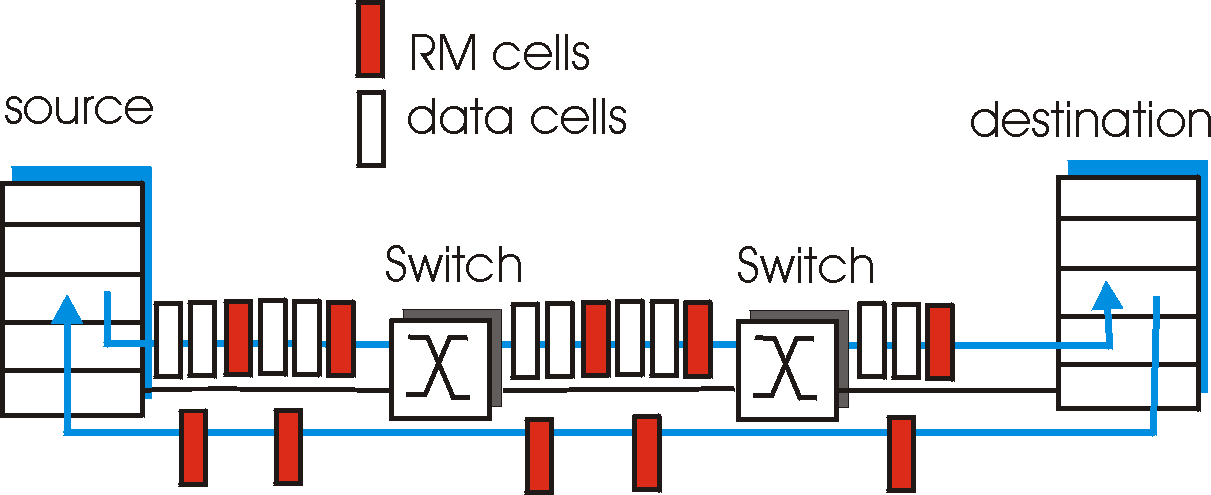
ATM ABR congestion control is a rate-based approach. That is, the sender explicitly computes a maximum rate at which it can send and regulates itself accordingly. ABR provides three mechanisms for signaling congestion-related information from the siwtches to the receiver: