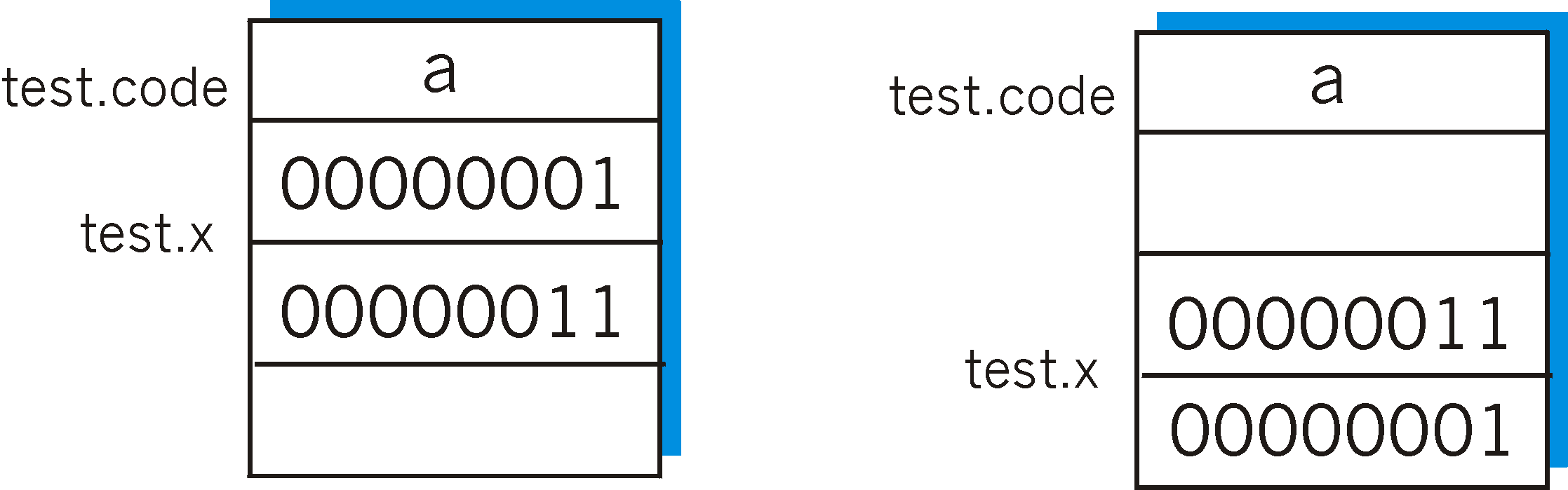
Figure 8.4-1: Two different data layouts on two different architectures
In order to motivate our discussion here, consider the following thought experiment. Suppose one could reliably copy data from one computer's memory directly into another remote computer's memory. If one could do this, would the communication problem be "solved?" The answer to the question depends on one's definition of "the communication problem". Certainly, a perfect memory-to-memory copy would exactly communicate the bits and bytes from one machine to another. But does such an exact copy of the bits and bytes mean that when software running on the receiving computer accesses this data, it will see the same values that were stored into the sending computer's memory? The answer to this question is "not necessarily"! The crux of the problem is that different computer architectures, different operating systems and compilers have different conventions for storing and representing data. If data is to be communicated and stored among multiple computers (as it is in every communication network!), this problem of data representation must clearly solved.
As an example of this problem, consider the simple C code fragment below. How might this structure be laid out in memory?
struct {
char code;
int x;
} test;
test.x = 259;
text.c = 'a';

The left side of Figure 8.4-1 shows a possible layout of this data on one hypothetical architecture: there is a single byte of memory containing the character 'a', followed by a 16-bit word containing the integer value 259, stored with the most significant byte first. The layout in memory on another computer is shown in the right half of Figure 8.4-1: the character 'a' is followed by the integer value stored with the least significant byte stored first and with the 16-bit integer aligned to start on a 16-bit word boundary. Certainly, if one were to perform a verbatim copy between these two computers' memories and use the same structure definition to access the stored values, one would see very different results on the two computers!
The problem of different architectures having a different internal data format is a real and pervasive problem. The particular problem of integer storage in different formats in different architectures is so common that it has a name. "Big-endian" order for storing integers has the most significant bytes of the integer stored first (at the lowest storage address). "Little-endian" order stores the least significant bytes first. Sun SPARC and Motorola processors are big-endian, while Intel and DEC Alpha processors are little endian. As an aside, the terms "big-endian" and "little-endian" come from the book, "Gullivers Travel's" by Jonathan Smith, in which two groups of people dogmatically insist on doing a simple thing is two different ways (hopefully, the analogy to the computer architecture community is clear). One group in the land of Lilliput insists on breaking their eggs at the larger end ("the big endians"), while other insists on breaking them at the smaller end. The difference was the cause of great civil strife and rebellion.
Given that different computers store and represent data in different ways, how should networking protocols deal with this? For example, if an SNMP agent is about to send a Response message containing the integer count of the number of received UDP datagrams, how should the represent the integer value to be sent to the managing entity - in big endian or little endian order? One option would be for the agent to send the bytes of the integer in the same order in which they would be stored in the managing entity. Another option would be for the agent to send in its own storage order and have the receiving entity reorder the bytes, as needed. Either option would require the sender or receiver to learn the other's format for integer representation.
A third option is to have a machine-, OS-, language-independent method
for describing integers and other data types (i.e., a data
description language) and rules that state the manner in which each of
the data types are to be transmitted over the network. When data of a given
type is received, it is received in an known format and can then be stored
in whatever machine-specific format is required. Both the SMI that we studied
in section 8.3 and ASN.1 adopt this third option. In ISO parlance,
these two standards describe a presentation service - the service
of transmitting and translating information from one machine-specific format
to another. Figures 8.4-2 illustrates a real-world presentation problem;
neither receiver understands the essential idea being communicated - that
the speaker likes something. As shown in Figure 8.4-3, a presentation
service can solve this problem by translating the idea into a commonly
understood (by the presentation service), person-independent language,
sending that information to the receiver, and then translating into a language
understood by the receiver.
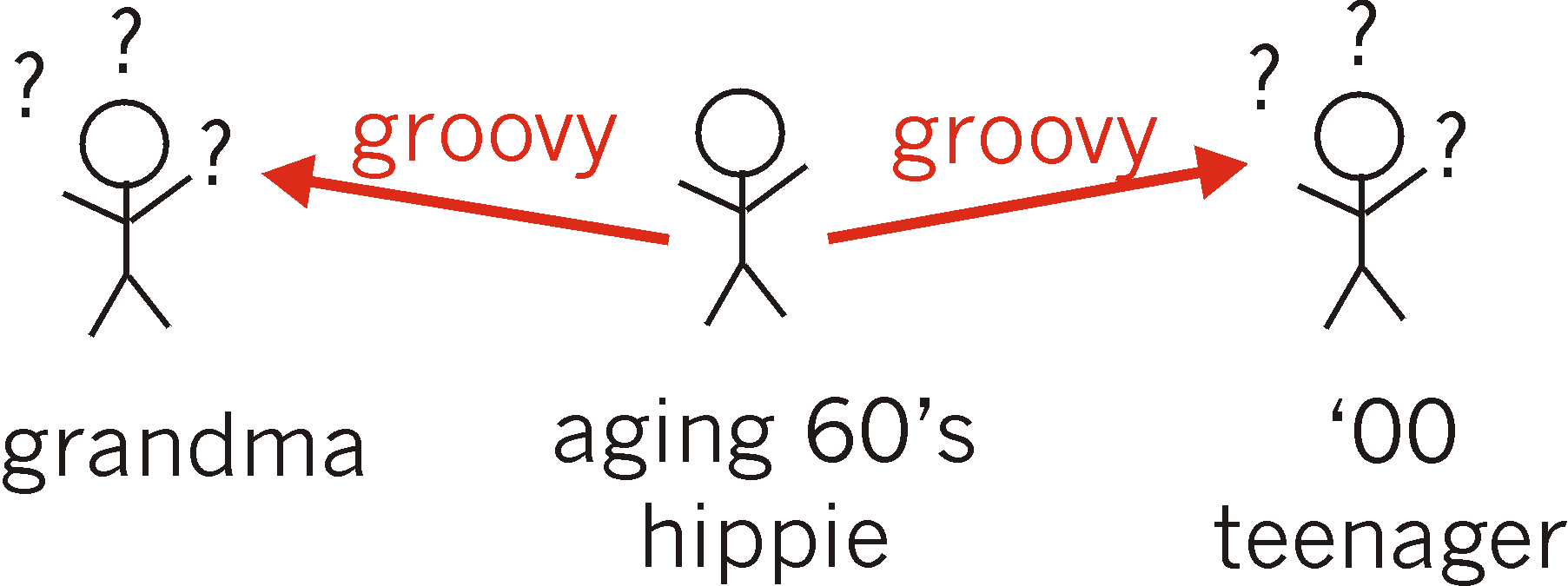
Figure 8.4-2: The presentation problem
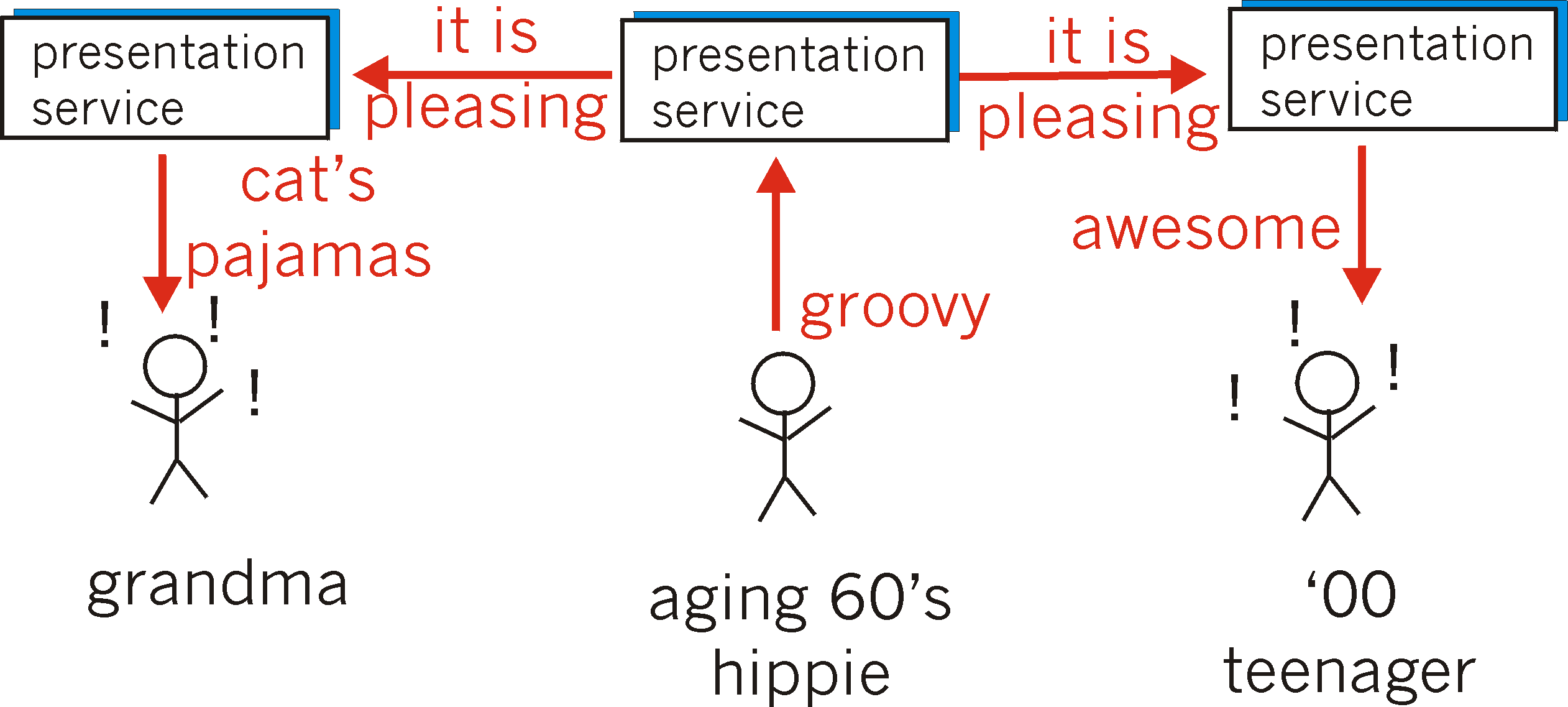
Figure 8.4-3: The presentation problem solved
Table 8.4-1 shows a few of the ASN.1 defined data types. Recall that
we encountered the INTEGER, OCTET STRING and OBJECT IDENTIFIER data types
in our earlier study of the SMI. Since our goal here is (mercifully) not
to provide a complete introduction to ASN.1, we refer the reader to the
standards or to the printed and on-line book [Larmouth
1996]
for a description of ASN.1 types and constructors such as SEQUENCE
and SET that allow for the definition of more structures.
| Tag | Type | Description |
| 1 | BOOLEAN | value is "true" or "false" |
| 2 | INTEGER | can be arbitrarily large |
| 3 | BITSTRING | list of one or more bits |
| 4 | OCTET STRING | list of one or more bytes |
| 5 | NULL | no value |
| 6 | OBJECT IDENTIFIER | name, in the ASN.1 standard naming tree, see section 8.2.2 |
| 9 | REAL | floating point |
In addition to providing a data description language, ASN.1 also provides Basic Encoding Rules (BER) that specify how instances of objects that have been defined using the ASN.1 data description language are to be sent over the network. The BER adopts a so-called TLV (Type, Length, Value) approach to encoding data for transmission. For each data item to be sent, the data type, the length of the data item, and then the actual value of the data item are sent, in that order. With this simple convention, the received data is essentially self identifying.
Figure 8.4.4 shows how the two data items in our simple C-language example
above would be sent. In this example, the sender wants to send the
letter 'a' followed by the value 259 decimal (which equals 00000001 00000011
in binary, or a byte value of 1 followed by a byte value of 3) assuming
big-endian order. The first byte in the transmitted stream has the value
4, indicating that the type of the following data item is an OCTET
STRING; this is the 'T' in the TLV encoding. The second byte in the
stream contains the length of the OCTET STRING, in this case 1. The
third byte in the transmitted stream begins (and ends) the OCTET STRING
of length one; it contains the ASCII representation of the letter 'a'.
The T, L, and V values of the next data item are 2 (the INTEGER type
tag value), 2 (i.e., an Integer of length 2 bytes), and the two-byte big-endian
representation of the value 259 decimal).
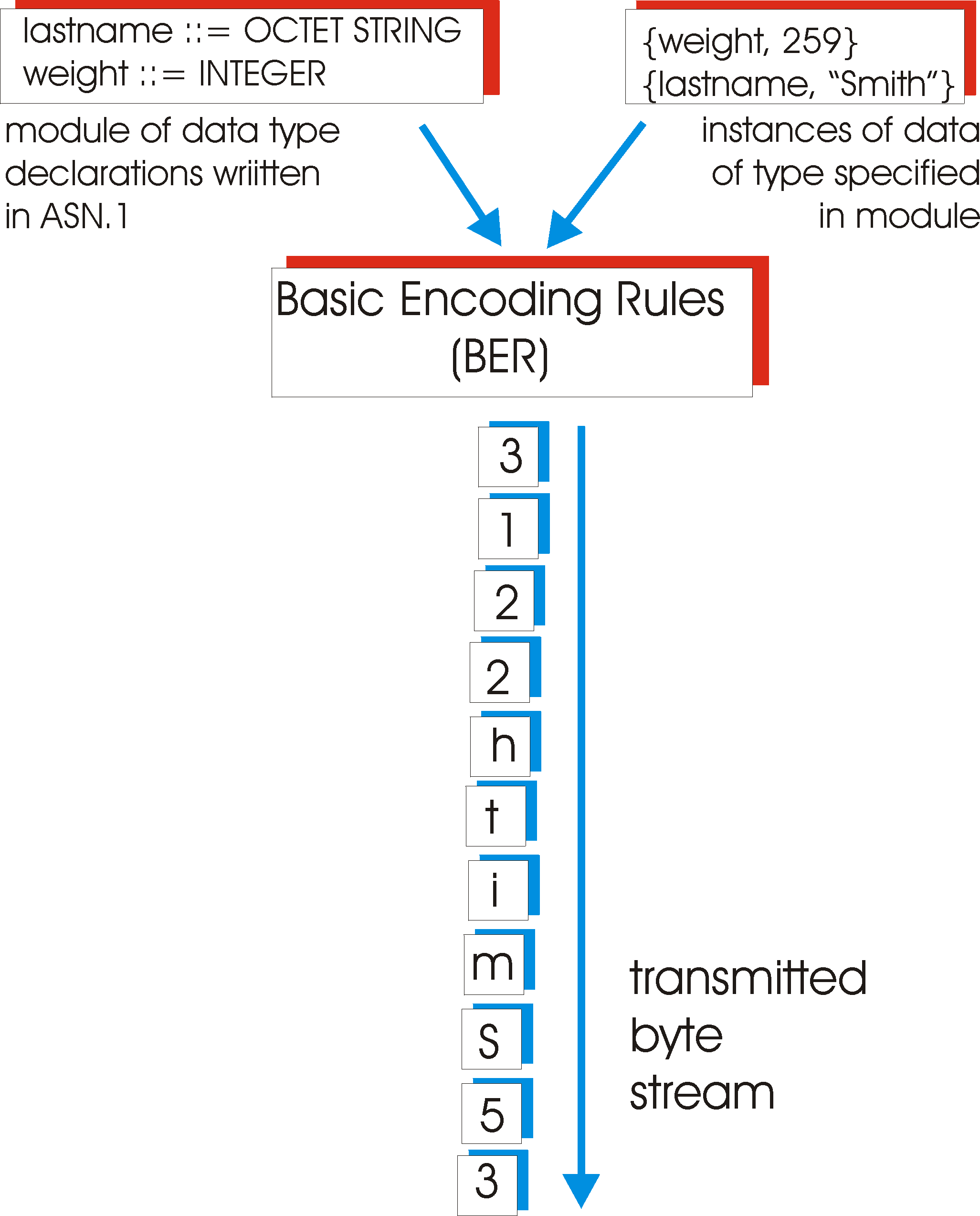
Figure 8.4-4: BER encoding example
In our discussion above, we have only touched on a small and simple
subset of ASN.1. Resources for learning more about ASN.1 include the ASN.1
standards document [ISO 1987,
ISOX.680], Philipp Hoschka's ASN.1 homepage [Hoschka
1997], and [Larmouth 1996].
Copyright 1999. James F. Kurose and Keith W. Ross. All Rights Reserved.